貝茲曲線:修訂版本之間的差異
出自六年制學程
(→(三)求端點的切線斜率) |
(→(五)總結) |
||
| 第 90 行: | 第 90 行: | ||
#t=<span style='font-stretch:condensed;'>½</span> 時弦垂直距離最大 | #t=<span style='font-stretch:condensed;'>½</span> 時弦垂直距離最大 | ||
#Q=<span style='font-stretch:condensed;'>½ </span>(P+P<sub>1</sub>) ,P,Q,P<sub>1</sub>,三點共線,且 Q 為 <span style='text-decoration:overline'>PP<sub>1</sub></span> 的中點。 | #Q=<span style='font-stretch:condensed;'>½ </span>(P+P<sub>1</sub>) ,P,Q,P<sub>1</sub>,三點共線,且 Q 為 <span style='text-decoration:overline'>PP<sub>1</sub></span> 的中點。 | ||
| − | #<span | + | #<span class='overline-segment'>P<sub>1</sub>P<sub>0</sub></span>, <span class='overline-segment'>P<sub>1</sub>P<sub>2</sub></span> 分別切二次貝茲曲線 P<sub>0</sub>QP<sub>2</sub> 於 P<sub>0</sub>, P<sub>2</sub> |
#二次貝茲曲線 P<sub>0</sub>QP<sub>2</sub> 為拋物線。 | #二次貝茲曲線 P<sub>0</sub>QP<sub>2</sub> 為拋物線。 | ||
2023年9月19日 (二) 10:54的修訂版本
目錄
一次貝茲曲線

B(t)=P0+(P1-P0)t=(1-t)P0+tP1, t∈[0,1]
B(t)描述一條由P0至P1的直線。例如當t=0.25時,B(t)即一條由點P0至P1路徑的四分之一處。
等同於線性插值。
二次貝茲曲線
| 二次貝茲曲線的結構 |
|---|
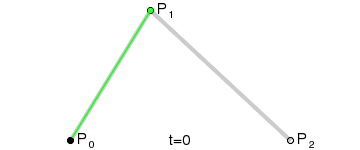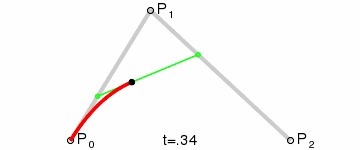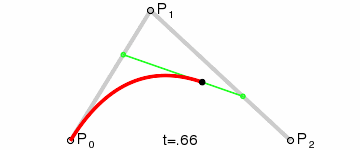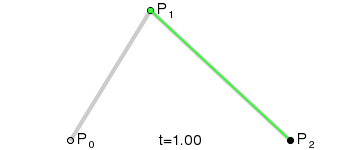 |
| 二次貝茲曲線演示 t在[0,1]區間 |
重點:
- 二次貝茲曲線畫出的是拋物線,無法畫出橢圓和雙曲線。故無法畫出正圓。
- 所有拋物線都「相似」(不是相等),且所有曲率(0~∞)的微線段都有。
- 兩端點外只有一個控制點。
- 拋物線方程式 ax2+bxy+cy2+dx+ey+f=0 則 b2 - 4ac=0 ,即前三項為完全平方式。
由二次貝茲曲線參數方程推導出四性質
- 二次貝茲曲線是拋物線
- t=½ 時弦垂直距離最大
- 弦中點、與弦垂直距離最大點(簡稱弦高點)、控制點三點共線,且弦高點為弦中點與控制點的中點。
- 控制點與兩端點連線分別切二次貝茲曲線於兩端點。
二次貝茲曲線的參數方程為:
B(t)=(1−t)2×P0+2(1−t)t×P1+t2×P2, t∈[0,1]
將弦水平放置後,其中:
- t 是一個介於 0 到 1 之間的參數
- P0 是起點,座標設為 (0,0)
- P1 是控制點,座標設為 (α,β)
- P2 是終點,座標設為 (ɭ,0)
圖形為:
我們讓起迄點水平排列,並準備由控制點座標(α,β),求出最低點座標(a,b)。
為了找到最大和最小的 y 值,我們可以對 y 的方程進行微分,並將其設為 0 以找到可能的極值。
(一)先求控制點與最低點的 y 值關係
將控制點的 y 值代入 By(t) 的方程式,我們得到:
- By(t)=(1−t)2×0+2(1−t)t×β+t2×0=2β×t(1−t)=2β×(t−t2)
對其進行微分:
- By′(t)=2β(1-2t)
將斜率設為 0 以解 t:
- 1−2t=0
- t=½
將 t=½ 代入 By(t) ,我們得到:
- By(½)=2β(½)(½)=½ β
因此,最低點的 y 值是 ½ β 。
(二)次求控制點與最低點的 x 值關係:
起迄點水平排列時, y 的極值均在 t=½ 處。
由上一段推理得到 b=½ β,此時 t=½ 。
B(t)=(1−t)2×P0+2(1−t)t×P1+t2×P2, t∈[0,1]
Bx(½)=2(½)(½)α+(½)(½)ɭ=½ α+¼ ɭ=a
(三)求端點的切線斜率
切線斜率為 By′(t) / Bx′(t)=2β(1-2t) / 2α+2(ɭ-2α)t=β(1-2t) / α+(ɭ-2α)t
當 t=0 ,斜率為 β / α ,恰為 P1P0 的斜率
當 t=1 ,斜率為 -β / ɭ-α,恰為 P1P2 的斜率
<math>AB</math>
(四)二次貝茲曲線的圖形是拋物線
將起點、迄點、控制點的座標一般化:
- P0 座標 (x0,y0)
- P1 座標 (α,β)
- P2 座標 (x2,y2)
By(t)=(1−t)2×y0+2(1−t)t×β+t2×y2=y0+2(β-y0)t+(y0-2β+y2)t2
- By(t) 對 t 是一拋物線方程。
若 Bx(t) 為一線性函數,則 By(t) 將是一拋物線方程。
- 若 Bx(t) 為一線性函數,則 (x-x0)=t×(x2-x0)
- 代入 By(t) 得到將為 mx2+nx+ɭ 的形式,也是拋物線方程。
(五)總結
所以有:
- t=½ 時弦垂直距離最大
- Q=½ (P+P1) ,P,Q,P1,三點共線,且 Q 為 PP1 的中點。
- P1P0, P1P2 分別切二次貝茲曲線 P0QP2 於 P0, P2
- 二次貝茲曲線 P0QP2 為拋物線。
二次貝茲曲線在 SVG path 中的路徑表達語法
| Q or q (quadratic Bézier curve) |
x1 y1 x y <path d='M0,0 Q50,50 100,0' style='stroke:black'/> <path d='m0,0 q50,50 100,0' style='stroke:black'/> |
從目前點的座標畫條 二次貝茲曲線到指定 點的 x,y 座標:其中 x1,y1 為控制點 |
|
參考文章
- 貝茲曲線
- 連續平滑的貝塞爾曲線
- 二元二次方程式圖形判別的例題
---------- 擬合圓 ----------