使用者:莊坤霖：修訂版本之間的差異
出自六年制學程
| 第 26 行： | 第 26 行： | ||
∠H=∠F(對頂角相等)<br/> | ∠H=∠F(對頂角相等)<br/> | ||
<span style="text-decoration:overline">AD</span>=<span style="text-decoration:overline">BC</span><br/> | <span style="text-decoration:overline">AD</span>=<span style="text-decoration:overline">BC</span><br/> | ||
| + | |||
∠L=∠J(內錯角相等)<br/> | ∠L=∠J(內錯角相等)<br/> | ||
∠I=∠K(內錯角相等)<br/> | ∠I=∠K(內錯角相等)<br/> | ||
| − | + | 以上合起來是ASA | |
∴<span style="text-decoration:overline">IM</span>=<span style="text-decoration:overline">CM</span><br/> | ∴<span style="text-decoration:overline">IM</span>=<span style="text-decoration:overline">CM</span><br/> | ||
<span style="text-decoration:overline">DM</span>=<span style="text-decoration:overline">BM</span><br/> | <span style="text-decoration:overline">DM</span>=<span style="text-decoration:overline">BM</span><br/> | ||
2016年9月22日 (四) 14:47的修訂版本
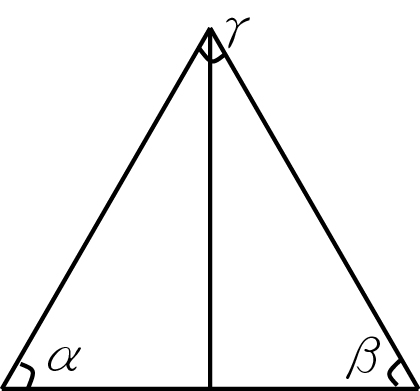
- 三角形的三外角之和是360°。
∠α+∠α'=180°
∠β+∠β'=180°
∠γ+∠γ'=180°
180°+180°+180°=540°
540°-內角和180°=360°
- 三角形的兩鄰邊之和大於第三邊，三角形的兩鄰邊之差小於第三邊
直線是以兩點最短的距離∴
AC+AB＞CB
AB+BC＞AC
移項
AC-AB＞CB
AB-BC＞AC
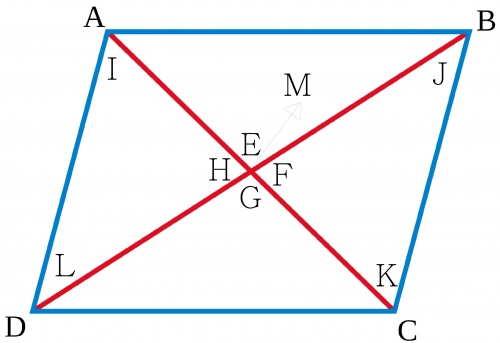
- ASA(角邊角)：有兩角及其夾邊對應相等的兩個三角形全等。
如果ΗΓ不重合ΑΓ∠Γ就不相等
此為正三角形∴三邊為60°，中間切半就是直角三角形∴γ為30°。
∠H=∠F(對頂角相等)
AD=BC
∠L=∠J(內錯角相等)
∠I=∠K(內錯角相等)
以上合起來是ASA
∴IM=CM
DM=BM
