「使用者:莊坤霖」修訂間的差異
跳至導覽
跳至搜尋
| 第9行: | 第9行: | ||
*三角形的兩鄰邊之和大於第三邊,三角形的兩鄰邊之差小於第三邊<br/> | *三角形的兩鄰邊之和大於第三邊,三角形的兩鄰邊之差小於第三邊<br/> | ||
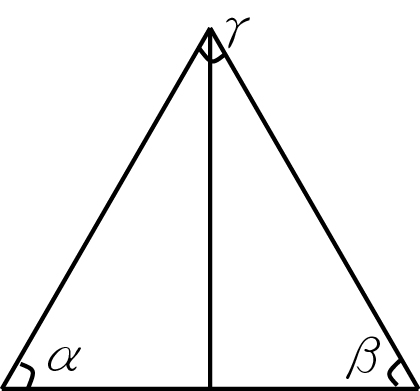
[[File:Rtriangle.svg|500px]]<br/> | [[File:Rtriangle.svg|500px]]<br/> | ||
| − | + | 直線是以兩點最短的距離∴<br/> | |
<span style="text-decoration:overline">AC</span>+<span style="text-decoration:overline">AB</span>><span style="text-decoration:overline">CB</span><br/> | <span style="text-decoration:overline">AC</span>+<span style="text-decoration:overline">AB</span>><span style="text-decoration:overline">CB</span><br/> | ||
<span style="text-decoration:overline">AB</span>+<span style="text-decoration:overline">BC</span>><span style="text-decoration:overline">AC</span><br/> | <span style="text-decoration:overline">AB</span>+<span style="text-decoration:overline">BC</span>><span style="text-decoration:overline">AC</span><br/> | ||
於 2016年9月18日 (日) 10:37 的修訂
- 三角形的三外角之和是360°。
500px
∠α+∠α'=180°
∠β+∠β'=180°
∠γ+∠γ'=180°
180°+180°+180°=540°
540°-內角和180°=360°
- 三角形的兩鄰邊之和大於第三邊,三角形的兩鄰邊之差小於第三邊
500px
直線是以兩點最短的距離∴
AC+AB>CB
AB+BC>AC
移項
AC-AB>CB
AB-BC>AC
- ASA(角邊角):有兩角及其夾邊對應相等的兩個三角形全等。
檔案:Congruence of triangles ASA.png
如果ΗΓ不重合ΑΓ∠Γ就不相等
此為正三角形∴三邊為60°,中間切半就是直角三角形∴γ為30°。